
本ページでは、プロビットモデル・ロジットモデルの概要についてまとめたい。
両モデルは、ダミー変数(1または0のみをとる変数)を被説明変数とした場合に、説明変数との関係を説明する際に用いる。
例えば合格・不合格、犯罪歴の有り・無しといった二つの値のどちらかしかとらないような事項が、どんな変数に影響を受けているのかを見たい場合、被説明変数にダミー変数を置くことが有効となる。
線形確率モデル
ロジット、プロビットの話に入る前に、線形確率モデルから説明を始めたい。線形確率モデルとは、通常の回帰分析とは基本的に全く同じで、ただ被説明変数をダミー変数にしたものである。この場合、被説明変数の条件付期待値は被説明変数が1となる確率を表現している。
線形確率モデルにおける回帰係数の解釈は、説明変数が1単位増加したときに被説明変数が1になる確率がどれほど変化するか、ということになる。
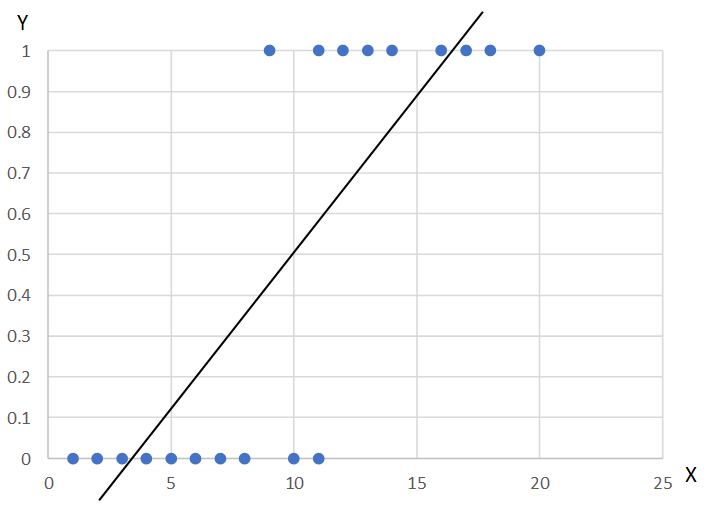
線形確率モデルのメリットは、通常の回帰分析の延長で行うことができ、回帰係数の解釈もわかりやすいという点にある。一方、このモデルにおいては、モデルが予測する被説明変数の値が、0から1以外の値をとってしまうことも考えられる。以下の図は線形確率モデルのイメージ図である。青い点は観測値で、黒い線が回帰式によるYの推定値となる。
プロビットモデル
線形確率モデルの限界(被説明変数の推定値が0から1以外の値をとってしまう可能性があることなど)を克服したのが、プロビットモデル、ロジットモデルと言える。これらは、Yが0から1以外の値を取らないような制約が課されているモデルとなっている。より具体的には、被説明変数は「Y=1となる確率」ということになる。
プロビットモデルは以下のように表すことができる。
![]()
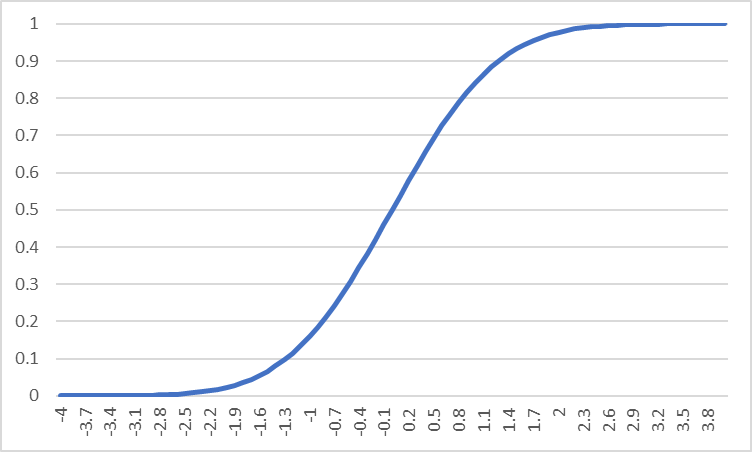
Φは、標準正規分布の累積分布関数である(下図)。横軸は確率変数zとなる。zの各値に対応する縦軸の値は「zがその値以下となる確率」である。
ロジットモデル
ロジットモデルはプロビットモデルと似ているが、プロビットモデルでは標準正規分布の累積分布関数が用いられたのに対し、ロジットモデルではロジスティック分布の累積分布関数が用いられる。数式は以下の通りとなる。
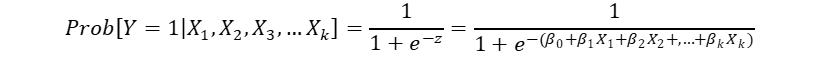
標準正規分布とロジスティック分布は似たものとなっているが、ロジスティック分布の方がより裾野が広くなっている。
計算の方法
ではどのようにしてβを推定するのだろうか。推定にあたっては、最尤法という手法を用いる。最尤法の基本的な考え方については以下を参照されたい。
ここではプロビットモデルを例にとって説明する。大学の合格(Y=1)・不合格(Y=0)に関するサンプルデータを集め、(1,1,0)というサンプルが集まったとする。
標準正規分布の累積分布関数に従うと仮定すると、尤度関数LはL=φ(1)×φ(1)×φ(0)となる。φのパラメータは、上記の数式の通りβとなる(0〜kの計k+1個のパラメータ。)この尤度関数Lが最大になるようなパラメータを求める。
係数の解釈
ロジット、プロビットモデルにおいては、線形の回帰分析とは異なり、回帰係数の大きさを単純に解釈することはできない。Xが1単位増えたときにYはβだけ増える、、といった説明はできない。
説明変数Xの変化によって、Y=1である確率がどれほど変わるか、という限界効果を測定するのが、ロジット、プロビットモデルの主要な目的となる。被説明変数であるPr[Y=1]をXで微分した値を求めることによって、限界効果を求めることができる。
(参考):