
本ページでは、最小二乗推定量を行列とベクトルを用いて表現する方法についてまとめたい。具体的には、回帰式
の推定量を行列とベクトルを用いて表現してみる。
行列のおさらい
まず、本題に入る前に、行列のおさらいを簡単に行う。
行列の積
行列の積は以下のように計算できる。

ある行列の行(横)の本数をa、列(縦)の本数をbとして、行列の型を(a,b)で表すとする。このとき、A,B2つの行列の積ABを定義できるのは、
A:(l,m)
B:(m,n)
となる場合、すなわち(l,m)×(m,n)=(l,n)となり、Aの列の本数とBの行の本数が等しくなる場合のみである。2つの行列の積によって計算された新たな行列は、Aの行の本数×Bの列の本数となる。
単位行列
正方行列(行と列の数が同じ行列)の対角線上の要素(対角要素)がすべて1で、それ以外の要素がすべて0のものを単位行列と呼ぶ。
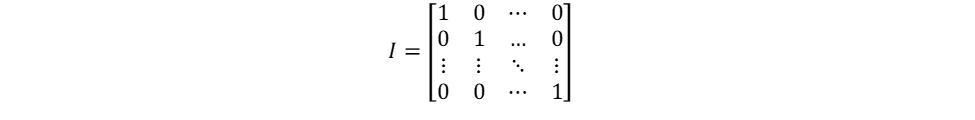
逆行列
正方行列Aについて、
![]()
となるような行列A^-1をAの逆行列という。2×2の場合の逆行列は以下の通りである。

なお、ad-bcの値は2次正方行列における行列式といい、|A|またはdet Aといった表記の仕方がある。3次以降の正方行列においても行列式は存在するが、計算はより複雑になる。行列式がゼロの場合は逆行列は存在しない。常に逆行列が存在するとは限らない。
Aの逆行列は、Aの余因子行列を行列式で除すことで計算できる。余因子行列は、以下の手順で求められる。
①Aの(i,j)成分の余因子を求める。余因子は、Aのi列とj列を取り除いた行列の行列式に、ー1のi+j乗を乗じたものになる。
例えば、

の(2,2)余因子は、

となる。
②Aの各成分における余因子で行列を構成する。例えば(1,1)成分に(1,1)余因子、(2,3)成分に(2,3)余因子をおく。次に、この行列の行と列を入れ替えると(転置)、余因子行列が完成する。転置については後述を参照。
転置
続いて、行列の転置について簡単におさらいしたい。行列の転置とは行と列を入れ替えることである。行列Xを転置したものはX’と表現される。例えば、

となる。
列ベクトルの転置×列ベクトルは要素の2乗和になる。つまり、

列ベクトル×行ベクトルは行列になる。

回帰式のベクトル表示
以下の回帰式をベクトル・行列を用いて表現する。
![]()
なお、i=1, ... ,n である。
まず、n個の観測値が存在するとき、上記の回帰式における各変数とパラメータを、ベクトルを用いて以下のように表現すると、

回帰式は次のように表せる。
![]()
Xはn行2列の行列となる。そして、最小二乗推定量とは、残差eの2乗和を最小にするように選んだβの値である。
残差二乗和は、残差ベクトルを用いるとe'eと書ける。
射影
最小二乗法を幾何的に考えると、以下の図のようになる。

残差の2乗は、ベクトルeの長さの2乗となる。最小二乗推定量は、幾何的には、ベクトルYとベクトルXの定数倍(β倍)の距離が最小になるようなβということになる。(このときのXβは、元の回帰式を思い出すと、Yの推定値(Y^)と等しくなっていることが分かる。)最小になるときのeは、上記の図の通り、Xの定数倍と直交(垂直に交わる)していることが分かる。
最小二乗推定量
2つのベクトルが直交しているとき、内積は0になる必要があるため、X'・e=X'・(Y-Xβ)=0となる。
このとき、最小二乗推定量は、
![]()
となる。
最後に、冒頭の回帰式の最小二乗推定量を行列を使わずに表現し直してみる。

であり、

となる。そして、

したがって、

説明変数Xの係数であるβ_2の値は、

となる。
(出典):