
本ページでは、均一なローンから構成される与信ポートフォリオの損失分布の推計について検討したい。
まず、与信ポートフォリオの信用リスクについて、1ファクターマートンモデルを用いた推計方法を以下のページで紹介している。本ページはこれに基づいており、数式の表記法も同様である。
マーケットファクターmが与えられた時の企業iにおける条件付デフォルト確率π(m)は
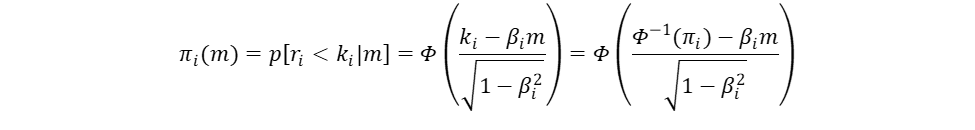
となる。このπ(m)を、以下では便宜的にpとする。
以下、全ての与信先企業のローン残高、デフォルト確率π、デフォルト時損失率が均一な場合を考える。
この場合、ローン数がn、デフォルト数をkとすると、ポートフォリオの中でk本のローンがデフォルトする確率は、以下の二項分布で表現することができる。
![]()
なお、この二項分布の期待値(つまりポートフォリオの期待損失率)はnpとなる。以下のグラフは、個々のローンのデフォルト確率が4%、デフォルト相関がゼロ、ローン数500の場合の与信ポートフォリオの損失分布である。

横軸はローン総数に占めるデフォルト数の割合(つまりp)である。
以下は、縦軸を累積分布関数にした場合である。

この損失分布から、期待損失やバリュー・アット・リスク(95%や99%水準など)を求めることが可能となる。例えば、信頼水準99%のバリュー・アット・リスク(VaR)を求める際には、累積分布関数の縦軸の値が0.99になる点に対応する横軸の値が、99%信頼水準における最大の損失割合(ローン総数に占めるデフォルト数)であり、ここからVaRを計算することができる。