
本ページでは、行列の基本的な計算についてまとめたい。具体的には、行列の積、単位行列、逆行列、転置について取り扱う。
行列の積
行列の積は以下のように計算できる。

ある行列の行(横)の本数をa、列(縦)の本数をbとして、行列の型を(a,b)で表すとする。このとき、A,B2つの行列の積ABを定義できるのは、
A:(l,m)
B:(m,n)
となる場合、すなわちAの列の本数とBの行の本数が等しくなる場合のみである。このとき、(l,m)×(m,n)=(l,n)となり、2つの行列の積によって計算された新たな行列は、Aの行の本数×Bの列の本数となる。
単位行列
正方行列(行と列の数が同じ行列)の対角線上の要素(対角要素)がすべて1で、それ以外の要素がすべて0のものを単位行列と呼ぶ。
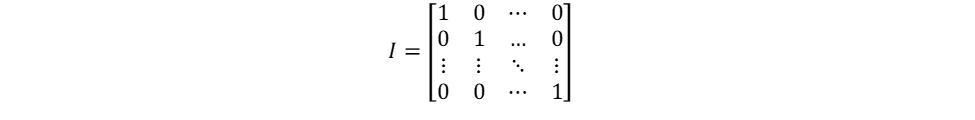
逆行列
正方行列Aについて、
![]()
となるような行列A^-1をAの逆行列という。2×2の場合の逆行列は以下の通りである。

なお、ad-bcの値は2次正方行列における行列式といい、|A|またはdet Aといった表記の仕方がある。3次以降の正方行列においても行列式は存在するが、計算はより複雑になる。行列式がゼロの場合は逆行列は存在しない。常に逆行列が存在するとは限らない。
Aの逆行列は、Aの余因子行列を行列式で除すことで計算できる。余因子行列は、以下の手順で求められる。
①Aの(i,j)成分の余因子を求める。余因子は、Aのi列とj列を取り除いた行列の行列式に、ー1のi+j乗を乗じたものになる。
例えば、

の(2,2)余因子は、

となる。
②Aの各成分における余因子で行列を構成する。例えば(1,1)成分に(1,1)余因子、(2,3)成分に(2,3)余因子をおく。次に、この行列の行と列を入れ替えると(転置)、余因子行列が完成する。転置については後述を参照。
転置
行列の転置とは行と列を入れ替えることである。行列Xを転置したものはX’と表現される。例えば、

となる。
列ベクトルの転置×列ベクトルは要素の2乗和になる。つまり、

列ベクトル×行ベクトルは行列になる。
